Los ejemplos citados
tienen un elemento en común, pueden ser descritos por una variable aleatoria
discreta que asume valores enteros (0, 1, 2, 3, 4, 5 y así sucesivamente).
La Distribución de
Poisson se llama así en honor a Simeón Dennis Poisson (1781-1840), francés que
desarrolló esta distribución basándose en estudios efectuados en la última
parte de su vida.
El número de enfermos
que llegan a un consultorio en cierto intervalo de tiempo será de 0, 1, 2, 3,
4, 5 o algún otro número entero. De manera análoga, si se cuenta el número de
automóviles que llegan a una caseta de cobro durante un periodo de diez
minutos, el número será entero.
El número de vehículos
que pasan por una caseta de cobro en las horas de mayor tráfico sirve como
ejemplo para mostrar las características de una distribución de probabilidad de
Poisson.
El promedio (media) de
los arribos de vehículos por hora de gran tráfico puede estimarse a partir de
los datos anteriores del tráfico.
Si dividimos las horas
de gran tráfico en periodos (intervalos) de un segundo cada uno, encontraremos
que los siguientes enunciados son verdaderos:
a) La probabilidad de
que exactamente un vehículo llegue por segundo a una caseta individual es un
número muy pequeño y es constante para que cada intervalo de un segundo.
b) La probabilidad de
que dos o más vehículos lleguen en un intervalo de un segundo es tan reducida
que podemos asignarle un valor cero.
c) El número de
vehículos que llegan en determinado intervalo de un segundo es independiente
del momento en que el intervalo de un segundo ocurre durante la hora de gran
tráfico.
d) El número de
llegadas en cualquier intervalo de un segundo no depende del número de arribos
de cualquier otro intervalo de un segundo.
Ahora bien, podemos
generalizar partiendo de las cuatro condiciones que hemos descrito en este
ejemplo, si estas condiciones se cumplen nos apoyaremos en una distribución de
probabilidad de Poisson para describirlos.
Sumas de variables
aleatorias de Poisson.
La suma de variables aleatorias de Poisson
independientes es otra variable aleatoria de Poisson cuyo parámetro es la suma
de los parámetros de las originales. Dicho de otra manera, si
Son N variables aleatorias de
Poisson independientes, entonces
Propiedades:
La función de masa o probabilidad de la distribución de Poisson es
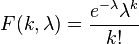
donde
- k es el número de ocurrencias del evento o fenómeno (la función nos da la probabilidad de que el evento suceda precisamente k veces).
- λ es un parámetro positivo que representa el número de veces que se espera que ocurra el fenómeno durante un intervalo dado. Por ejemplo, si el suceso estudiado tiene lugar en promedio 4 veces por minuto y estamos interesados en la probabilidad de que ocurra k veces dentro de un intervalo de 10 minutos, usaremos un modelo de distribución de Poisson con λ = 10×4 = 40.
- e es la base de los logaritmos naturales (e = 2,71828...)
Tanto el valor esperado como la varianza de una variable aleatoria con distribución de Poisson son iguales a λ. Los momentos de orden superior son polinomios de Touchard en λ cuyos coeficientes tienen una interpretación combinatoria. De hecho, cuando el valor esperado de la distribución de Poisson es 1, entonces según la fórmula de Dobinski, el n-ésimo momento iguala al número de particiones de tamañon.
La moda de una variable aleatoria de distribución de Poisson con un λ no entero es igual a 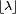 , el mayor de los enteros menores que λ (los símbolos
, el mayor de los enteros menores que λ (los símbolos  representan la función parte entera). Cuando λ es un entero positivo, las modas son λ y λ − 1.
La función generadora de momentos de la distribución de Poisson con valor esperado λ es
representan la función parte entera). Cuando λ es un entero positivo, las modas son λ y λ − 1.
La función generadora de momentos de la distribución de Poisson con valor esperado λ es

Las variables aleatorias de Poisson tienen la propiedad de ser infinitamente divisibles.
La divergencia Kullback-Leibler desde una variable aleatoria de Poisson de parámetro λ0 a otra de parámetro λ es

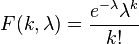
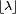 , el mayor de los enteros menores que λ (los símbolos
, el mayor de los enteros menores que λ (los símbolos  representan la función parte entera). Cuando λ es un entero positivo, las modas son λ y λ − 1.
representan la función parte entera). Cuando λ es un entero positivo, las modas son λ y λ − 1.

Intervalo de confianza
Un criterio fácil y rápido para calcular un intervalo de confianza aproximada de λ es propuesto por Guerriero (2012).1 Dada una serie de eventos k (al menos el 15 - 20) en un periodo de tiempo T, los límites del intervalo de confianza para la frecuencia vienen dadas por:


entonces los límites del parámetro  están dadas por:
están dadas por: .
.


 están dadas por:
están dadas por: .
.Relación con otras distribuciones
Sumas de variables aleatorias de Poisson
La suma de variables aleatorias de Poisson independientes es otra variable aleatoria de Poisson cuyo parámetro es la suma de los parámetros de las originales. Dicho de otra manera, si

son N variables aleatorias de Poisson independientes, entonces
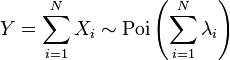 .
.

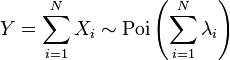 .
.Distribución binomial
La distribución de Poisson es el caso límite de la distribución binomial. De hecho, si los parámetros n y  de una distribución binomial tienden a infinito (en el caso de 'n') y a cero (en el caso de
de una distribución binomial tienden a infinito (en el caso de 'n') y a cero (en el caso de  ) de manera que
) de manera que  se mantenga constante, la distribución límite obtenida es de Poisson.
se mantenga constante, la distribución límite obtenida es de Poisson.
 de una distribución binomial tienden a infinito (en el caso de 'n') y a cero (en el caso de
de una distribución binomial tienden a infinito (en el caso de 'n') y a cero (en el caso de  ) de manera que
) de manera que  se mantenga constante, la distribución límite obtenida es de Poisson.
se mantenga constante, la distribución límite obtenida es de Poisson.Aproximación normal
Como consecuencia del teorema central del límite, para valores grandes de  , una variable aleatoria de Poisson X puede aproximarse por otra normal dado que el cociente
, una variable aleatoria de Poisson X puede aproximarse por otra normal dado que el cociente

converge a una distribución normal de media nula y varianza 1.
 , una variable aleatoria de Poisson X puede aproximarse por otra normal dado que el cociente
, una variable aleatoria de Poisson X puede aproximarse por otra normal dado que el cociente
Distribución exponencial
Supóngase que para cada valor t > 0, que representa el tiempo, el número de sucesos de cierto fenómeno aleatorio sigue una distribución de Poisson de parámetro λt. Entonces, los tiempos transcurridos entre dos sucesos sucesivos sigue la distribución exponencial.
Ejemplos
Si el 2% de los libros encuadernados en cierto taller tiene encuadernación defectuosa, para obtener la probabilidad de que 5 de 400 libros encuadernados en este taller tengan encuadernaciones defectuosas usamos la distribución de Poisson. En este caso concreto, k es 5 y, λ, el valor esperado de libros defectuosos es el 2% de 400, es decir, 8. Por lo tanto, la probabilidad buscada es




No hay comentarios:
Publicar un comentario